Section 2.4 Discriminative Data Prediction

The aforementioned X-risks can be unified under a principled discriminative learning framework for data prediction, providing a statistical foundation for developing advanced methods to train foundation models in modern AI.

The widely used foundation models include Contrastive Language-image Pretrained (CLIP) model (see Section 6.4), Dense Passage Retrieval (DPR) model, large language models (LLMs) such as the Generative Pretrained Transformer (GPT) series (see Section 6.5), and vision-language models (VLMs). These models fall into two main categories: representation models, such as CLIP and DPR, and generative models, including LLMs and VLMs.

We present a discriminative data prediction framework to facilitate the learning of these foundation models. Suppose there exists a set of observed paired data, \(\{(\mathbf{x}_i, \mathbf{y}_i)\}_{i=1}^n\), where \(\mathbf{x}_i \in \mathcal{X}\) and \(\mathbf{y}_i \in \mathcal{Y}\). These pairs typically represent real-world positive correspondences. While this setup resembles traditional supervised learning where \(\mathbf{x}_i\) represents input data and \(\mathbf{y}_i\) denotes a class label, there is a crucial difference: here, \(\mathbf{y}_i\) refers to data from a continuous space (e.g., images) or an uncountable space (e.g., text). For instance:

• In training the CLIP model, \(\mathbf{x}_i\) represents an image and \(\mathbf{y}_i\) is the corresponding text caption (or vice versa).
• In training the DPR model, \(\mathbf{x}_i\) is an input question, and \(\mathbf{y}_i\) is the corresponding textual answer.
• In fine-tuning LLMs or VLMs, \(\mathbf{x}_i\) represents input data (e.g., prompts or images), and \(\mathbf{y}_i\) represents the text to be generated.

Since the risk function usually involves coupling each positive data with many other possibly negative data points in a compositional structure, the resulting risk is called discriminative X-risk. The following subsections detail two specific approaches to formulating discriminative X-risk.

2.3.1 A Discriminative Probabilistic Modeling Approach

Without loss of generality, we assume that \(\mathcal{Y}\) is a continuous space. A discriminative probabilistic approach models the conditional probability \(p(\mathbf{y}|\mathbf{x})\) using a parameterized prediction function: \[\begin{align}\label{eqn:dpm} p_{\mathbf{w}}(\mathbf{y}|\mathbf{x}) = \frac{\exp(s(\mathbf{w}; \mathbf{x}, \mathbf{y})/\tau)}{\int_{\mathcal{Y}}\exp(s(\mathbf{w}; \mathbf{x}, \mathbf{y}')/\tau)d\mu(\mathbf{y}')}, \end{align}\] where \(\tau>0\) is a temperature hyperparameter, and \(\mu\) is the measure associated with the space \(\mathcal{Y}\). Given a set of observed positive pairs \(\{(\mathbf{x}_i, \mathbf{y}_i)\}_{i=1}^n\), the model parameters \(\mathbf{w}\) are learned by minimizing the empirical risk of the negative log-likelihood: \[ \min_{\mathbf{w}} -\frac{1}{n}\sum_{i=1}^n\tau \log \frac{\exp(s(\mathbf{w}; \mathbf{x}_i, \mathbf{y}_i)/\tau)}{\int_{\mathcal{Y}}\exp(s(\mathbf{w}; \mathbf{x}_i, \mathbf{y}')/\tau)d\mu(\mathbf{y}')}. \] A significant challenge in solving this problem lies in handling the partition function, \[ Z_i = \int_{\mathcal{Y}}\exp(s(\mathbf{w}; \mathbf{x}_i, \mathbf{y}')/\tau)d\mu(\mathbf{y}'), \] which is often computationally intractable. To overcome this, an approximation can be constructed using a set of samples \(\hat{\mathcal{Y}}_i \subseteq \mathcal{Y}\). The partition function is then estimated as: \[ \hat{Z}_i = \sum_{\hat{\mathbf{y}}_j\in\hat{\mathcal{Y}}_i}\frac{1}{q_j}\exp(s(\mathbf{w}; \mathbf{x}_i, \hat{\mathbf{y}}_j)/\tau), \] where \(q_j\) is an importance weight that accounts for the underlying measure \(\mu\). Consequently, the empirical X-risk minimization problem is reformulated as: \[ \min_{\mathbf{w}} \frac{1}{n}\sum_{i=1}^n\tau \log \left(\sum_{\hat{\mathbf{y}}_j\in\hat{\mathcal{Y}}_i}\exp((s(\mathbf{w}; \mathbf{x}_i, \hat{\mathbf{y}}_j)+\zeta_j-s(\mathbf{w}; \mathbf{x}_i, \mathbf{y}_i))/\tau)\right), \] where \(\zeta_j = \tau \ln \frac{1}{q_j}\).

Instantiation

The standard cross-entropy loss and the listwise cross-entropy loss are special cases of this framework, where \(\mathcal{Y}\) is either a finite set of labels or a list of items to be ranked for each query. In such cases, the integral reduces to a summation, and there is no need to approximate \(Z_i\). However, computing \(Z_i\) can still be challenging when \(\mathcal{Y}\) is large, motivating the development of advanced compositional optimization techniques.

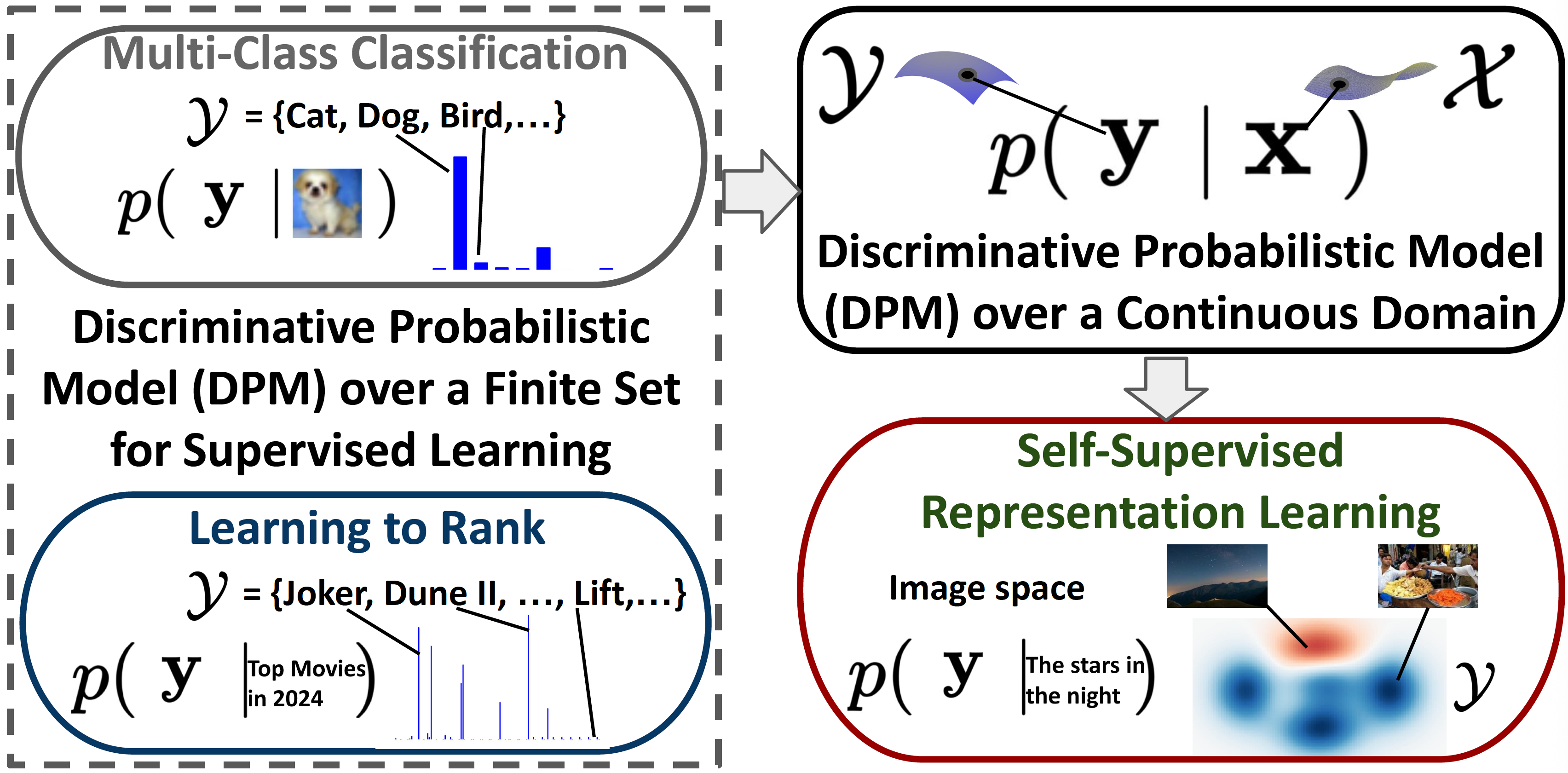
Contrastive losses of CLIP for multi-modal representation learning can also be interpreted within this framework. Let \(\mathbf{x}_i\) be an image and \(\mathbf{y}_i=\mathbf{x}_i^+\) be its corresponding text description, the output space \(\mathcal{Y}\) corresponds to the (potentially infinite) set of all texts. Let \(s(\mathbf{w}; \mathbf{x}, \mathbf{y}) = h_1(\mathbf{w}; \mathbf{x})^{\top}h_2(\mathbf{w}; \mathbf{y})\) be the similarity of two embedding vectors encoded by \(h_1\) on the image and \(h_2\) on the text. Then modeling \(p_{\mathbf{w}}(\mathbf{y}_i|\mathbf{x}_i)\) by (\(\ref{eqn:dpm}\)) with \(Z_i\) approximated using the observed set of texts \(\hat{\mathcal{Y}}_i = \mathcal{T}\) and uniform importance weights \(q_j\) yields the loss similar to Equation 21. Conversely, we can also model \(p_{\mathbf{w}}(\mathbf{x}_i|\mathbf{y}_i)\) similar to (\(\ref{eqn:dpm}\)) to define a symmetric contrastive loss with the text as the anchor space. An illustration of the connection between the probabilistic model for multi-modal representation learning and traditional supervised learning tasks including multi-class classification and learning to rank is shown in Figure 2.5.

Nevertheless, more accurate estimators of \(Z_i\) can be constructed using non-uniform weights \(q_j\), which may help reduce the generalization error of the learned model. We explore this approach and its applications to fine-tuning LLMs in Section 6.4.

2.4.2 A Robust Optimization Approach

The goal of discriminative learning is to increase the score \(s(\mathbf{w}; \mathbf{x}, \mathbf{y}_+)\) for a positive pair \((\mathbf{x}, \mathbf{y}_+) \sim \mathbb{P}_+(\mathbf{x}, \mathbf{y}_+)\) while decreasing the score \(s(\mathbf{w}; \mathbf{x}, \mathbf{y}_-)\) for any negative pair \((\mathbf{x}, \mathbf{y}_-) \sim \mathbb{P}_-(\mathbf{x}, \mathbf{y}_-)\).

Let \(\mathbb{P}_+(\mathbf{x}, \mathbf{y}_+) = \mathbb{P}(\mathbf{x})\mathbb{P}_+(\mathbf{y}_+|\mathbf{x})\), \(\mathbb{P}_-(\mathbf{x}, \mathbf{y}_-) = \mathbb{P}(\mathbf{x})\mathbb{P}_-(\mathbf{y}_-|\mathbf{x})\), and \(\mathbb{P}(\mathbf{x}, \mathbf{y}_+, \mathbf{y}_-) = \mathbb{P}_+(\mathbf{y}_+|\mathbf{x})\mathbb{P}_-(\mathbf{y}_-|\mathbf{x})\mathbb{P}(\mathbf{x})\). Define a pairwise loss as \(L(\mathbf{w}; \mathbf{x}, \mathbf{y}_+, \mathbf{y}_-) = \ell(s(\mathbf{w}; \mathbf{x}, \mathbf{y}_-) - s(\mathbf{w}; \mathbf{x}, \mathbf{y}_+))\).

Full Supervised Setting

Let us first consider the supervised learning setting, where positive and negative samples are true ones from their corresponding distributions. A naive goal is to minimize the expected risk: \[ \min_{\mathbf{w}} \mathbb{E}_{\mathbf{x}, \mathbf{y}_+, \mathbf{y}_- \sim \mathbb{P}(\mathbf{x}, \mathbf{y}_+, \mathbf{y}_-)} [\ell(s(\mathbf{w}; \mathbf{x}, \mathbf{y}_-) - s(\mathbf{w}; \mathbf{x}, \mathbf{y}_+))]. \]

However, a fundamental challenge for data prediction is that the number of negative data is usually much larger than the number of positive data. Hence, the expected risk is not a strong measure. To address this challenge, we can leverage DRO or OCE. In particular, we replace the expected risk \(\mathbb{E}_{\mathbf{y}_- \sim \mathbb{P}(\mathbf{y}_-|\mathbf{x})} [\ell(s(\mathbf{w}; \mathbf{x}, \mathbf{y}_-) - s(\mathbf{w}; \mathbf{x}, \mathbf{y}_+))]\) by its OCE counterpart, resulting in the following population risk: \[\begin{align} \min_{\mathbf{w}}\mathbb{E}_{\mathbf{x}, \mathbf{y}_+}\left[ \min_{\mu} \tau \mathbb{E}_{\mathbf{y}_-|\mathbf{x}}\phi^*\left(\frac{\ell(s(\mathbf{w}; \mathbf{x}, \mathbf{y}_-) - s(\mathbf{w}; \mathbf{x}, \mathbf{y}_+))- \mu}{\tau}\right) + \mu\right]. \end{align}\]

Its empirical version becomes: \[\begin{align}\label{eqn:soce-1} \min_{\mathbf{w}} \frac{1}{nK}\sum_{i=1}^n\sum_{k=1}^K\min_{\mu_{ik}} \tau \frac{1}{m}\sum_{j=1}^m\phi^*\left(\frac{\ell(s(\mathbf{w}; \mathbf{x}_i, \mathbf{y}_{ij}^-) - s(\mathbf{w}; \mathbf{x}, \mathbf{y}_{ik}^+))- \mu_{ik}}{\tau}\right) + \mu_{ik}. \end{align}\]

Semi-supervised Setting

We can extend the above framework to the semi-supervised learning setting (including the self-supervised setting), where we only have samples from the positive distribution \(P_+(\cdot|\mathbf{x})\) and the marginal distribution \(P(\cdot|\mathbf{x})\). In particular, the training dataset is \(\mathcal{S}=\{\mathbf{x}_i, \mathbf{y}^+_{ik}, \mathbf{y}_{ij}, i\in[n], j\in[m], k\in[K]\}\), where \(\mathbf{y}^+_{ik}\sim P_+(\cdot|\mathbf{x}_i)\) and \(\mathbf{y}_{ij}\sim P(\cdot|\mathbf{x}_i)\).

Let us assume that \(P(\cdot|\mathbf{x}) = \pi_+(\mathbf{x})P_+(\cdot|\mathbf{x}) + \pi_-(\mathbf{x})P_-(\cdot|\mathbf{x})\) and \(\pi_+(\mathbf{x})\ll\pi_-(\mathbf{x})\). This means that for a fixed data \(\mathbf{x}\), the sampled data \(\mathbf{y}\sim P(\cdot|\mathbf{x})\) is mostly likely from the negative distribution \(P_-(\cdot|\mathbf{x})\). Hence, we can approximate \(\mathbb{E}_{\mathbf{y}_-\sim P_-(\cdot|\mathbf{x})}\) by \(\mathbb{E}_{\mathbf{y}\sim P(\cdot|\mathbf{x})}\). Hence, a population risk in the self-supervised learning setting becomes: \[\begin{align} \min_{\mathbf{w}}\mathbb{E}_{\mathbf{x}, \mathbf{y}_+}\left[ \min_{\mu} \tau \mathbb{E}_{\mathbf{y}|\mathbf{x}}\phi^*\left(\frac{\ell(s(\mathbf{w}; \mathbf{x}, \mathbf{y}) - s(\mathbf{w}; \mathbf{x}, \mathbf{y}_+))- \mu}{\tau}\right) + \mu\right], \end{align}\] and its empirical version becomes: \[\begin{align}\label{eqn:soce-2} \min_{\mathbf{w}} \frac{1}{nK}\sum_{i=1}^n\sum_{k=1}^K\min_{\mu_{ik}} \tau \frac{1}{m}\sum_{j=1}^m\phi^*\left(\frac{\ell(s(\mathbf{w}; \mathbf{x}_i, \mathbf{y}_{ij}) - s(\mathbf{w}; \mathbf{x}, \mathbf{y}_{ik}^+))- \mu_{ik}}{\tau}\right) + \mu_{ik}. \end{align}\]

We refer to both the problem (\(\ref{eqn:soce-1}\)) and (\(\ref{eqn:soce-2}\)) as the Compositional OCE (COCE) optimization.

Instantiation

When \(\phi(t) = t\log t - t + 1\), the inner optimization over \(\mu\) in (\(\ref{eqn:soce-2}\)) admits a closed-form solution, which can be substituted back into the objective, yielding: \[\begin{align}\label{eqn:gcl-mu} \min_{\mathbf{w}} \frac{1}{nK} \sum_{i=1}^n \sum_{k=1}^K \tau \log\left( \frac{1}{m} \sum_{j=1}^m \exp\left( \frac{\ell(s(\mathbf{w}; \mathbf{x}_i, \mathbf{y}_{ij}) - s(\mathbf{w}; \mathbf{x}_i, \mathbf{y}_{ik}^+))}{\tau} \right) \right). \end{align}\]

This formulation unifies several well-known losses as special cases:

• Cross-Entropy Loss for Classification:
  Let \(\mathbf{x}_i\) denote an input data point, and let \(\mathbf{y}_{ik}^+\) (with \(k = 1\)) represent its true class label. Define the prediction score for the \(y\)-th class of \(\mathbf{x}\) as \(s(\mathbf{w}; \mathbf{x}, y) = h_0(\mathbf{w}_0; \mathbf{x})^{\top} \mathbf{w}_y\). When the loss function is \(\ell(s) = s\), the objective reduces to the empirical risk with the standard cross-entropy loss.

• Listwise Cross-Entropy Loss for Ranking:
  Let \(\mathbf{x}_i\) denote a query, \(\{\mathbf{y}_{ik}^+\}_{k=1}^K\) the set of relevant (positive) documents, and \(\{\mathbf{y}_{ij}\}_{j=1}^m\) the complete candidate list to be ranked. Let \(s(\mathbf{w}; \mathbf{x}, \mathbf{y})\) be the predicted relevance score between a query \(\mathbf{x}\) and a document \(\mathbf{y}\). When the loss function is \(\ell(s) = s\), the objective simplifies to the listwise cross-entropy loss.

• Self-supervised Contrastive Loss for Representation Learning:
  If \(\mathbf{x}_i\) is an anchor (e.g., an image), \(\mathbf{y}_{ik}^+\) denotes its positive pair (e.g., the corresponding text), and \(\{\mathbf{y}_{ij}\}_{j=1}^m\) denotes the set of all samples except for \(\mathbf{y}_{ik}^+\), the objective recovers the contrastive loss Equation 21 used in self-supervised contrastive representation learning.

• Partial AUC Loss for Imbalanced Binary Classification:
  Let \(\mathbf{x}_i\) be a fixed class label (\(i = 1\)), with \(\{\mathbf{y}_{ik}^+\}_{k=1}^K\) denoting its positive data set and \(\{\mathbf{y}_{ij}^-\}_{j=1}^m\) its negative data set. Define the score function as \(s(\mathbf{w}; \mathbf{x}, \mathbf{y}) = h(\mathbf{w}; \mathbf{y}) \in \mathbb{R}\). Under this setting, equation (\(\ref{eqn:soce-1}\)) reduces to the partial AUC loss in Equation 16.

This framework offers a flexible foundation for designing alternative contrastive objectives by varying the loss function \(\ell(\cdot)\), the divergence function \(\phi(\cdot)\), and the distributionally robust optimization (DRO) formulation, including its constrained variants.

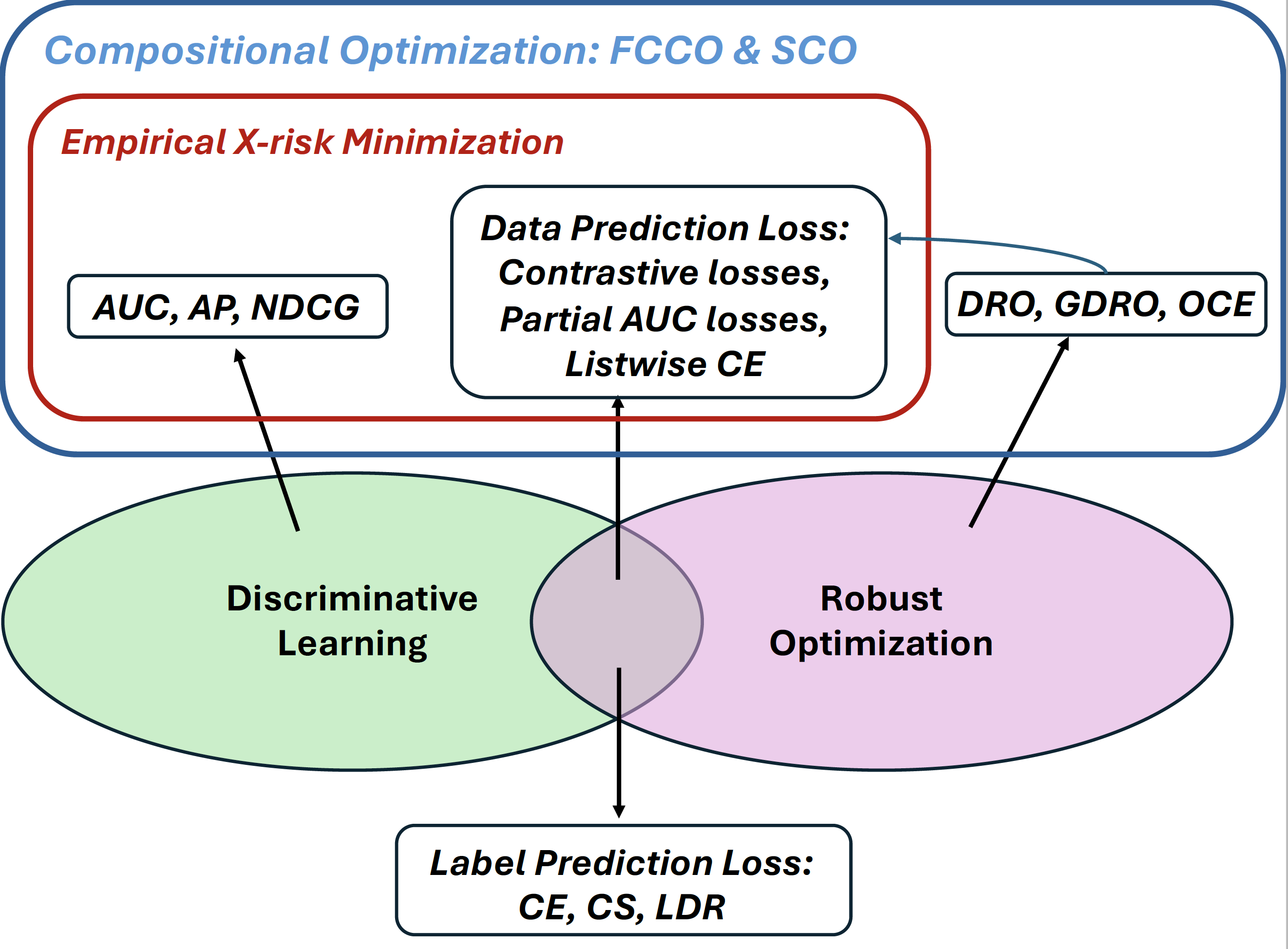
Finally, Figure 2.6 illustrates the losses, objectives, and learning frameworks discussed in this chapter, along with their connections to the principles of discriminative learning and robust optimization. This perspective highlights the necessity of stochastic compositional optimization and finite-sum coupled compositional optimization, which will be presented in subsequent chapters.