Empirical X-risk Minimization

So far, we have revisited classical ideas of machine learning based on empirical risk minimization and its distributionally robust variants. In these risk functions, we assume each data defines a loss based on itself. These losses are typically surrogate functions of a prediction error measuring the inconsistency between the prediction and the label.

However, such loss functions are insufficient to capture many objectives, which involve comparison between different data points. Examples include areas under ROC curves (AUROC) and areas under precision-recall curves (AUPRC) for imbalanced data classification, ranking measures such as normalized discounted cumulative gain (NDCG), mean average precision (MAP) and listwise losses for learning to rank, and contrastive losses for representation learning.

The standard ERM framework is inadequate for optimizing such metrics and losses, as they involve interactions across multiple data points. We need a new mathematical framework to understand the challenge and to design provable and practical algorithms. To this end, we introduce a new risk minimization framework, named empirical X-risk minimization (EXM), as defined below:

With \(g\) given in (\(\ref{eqn:avg-g}\)), EXM is an instance of finite-sum coupled compositional optimization (FCCO), a framework explored in detail in Chapter 5.

Below, we present several important instances of X-risks.

AUC Losses

AUC, short for Area under receiver operating characteristic (ROC) curve, is commonly used to measure performance for the imbalanced data classification.

Definition and an Empirical Estimator of AUC

The ROC curve is the plot of the true positive rate (TPR) against the false positive rate (FPR) at each threshold setting. Let \(\mathbb{P}_+,\mathbb{P}_-\) denote the distribution of random positive and negative data, respectively. Let \(h(\cdot):\mathcal{X}\to\mathbb{R}\) denote a predictive scoring function. For a given threshold \(t\), the TPR of \(h\) can be written as \(\text{TPR}(t)=\Pr(h(\mathbf{x})>t|y=1)=\mathbb{E}_{\mathbf{x}\sim\mathbb{P}_+}[\mathbb{I}(h(\mathbf{x})>t)]\), and the FPR can be written as \(\text{FPR}(t)=\Pr(h(\mathbf{x})>t|y=-1)=\mathbb{E}_{\mathbf{x}\sim\mathbb{P}_-}[\mathbb{I}(h(\mathbf{x})>t)]\). Let \(F_-(t)=1-\text{FPR}(t)\) denote the cumulative density function of the random variable \(h(\mathbf{x}_-)\) for \(\mathbf{x}_-\sim\mathbb{P}_-\). Let \(p_-(t)\) denote its corresponding probability density function. Similarly, let \(F_+(t)=1-\text{TPR}(t)\) and \(p_+(t)\) denote the cumulative density function and the probability density function of \(h(\mathbf{x}_+)\) for \(\mathbf{x}_+\sim\mathbb{P}_+\), respectively.

For a given \(u\in[0,1]\), let \(\text{FPR}^{-1}(u)=\inf\{t\in\mathbb{R}:\text{FPR}(t)\le u\}\). The ROC curve is defined as \(\{u,\text{ROC}(u)\}\), where \(u\in[0,1]\) and \(\text{ROC}(u)=\text{TPR}(\text{FPR}^{-1}(u))\).

Hence, we have the following theorem.

■

This indicates that AUC is a pairwise ranking metric. An ideal scoring function that ranks all positive examples above negative examples has a perfect AUC score \(1\). It also implies the following empirical non-parametric estimator of AUC based on a set of data \(\mathcal{S}\) with \(n_+\) positive samples in \(\mathcal{S}_+\) and \(n_-\) negative samples in \(\mathcal{S}_-\): \[\begin{align}\label{eqn:auc-emp} \text{AUC}(h;\mathcal{S})=\frac{1}{n_+n_-}\sum_{\mathbf{x}_+\in\mathcal{S}_+,\mathbf{x}_-\in\mathcal{S}_-}\mathbb{I}(h(\mathbf{x}_+)>h(\mathbf{x}_-)), \end{align}\] which is also known as the Mann-Whitney U-statistic (Hanley and McNeil, 1982).

Necessity of Maximizing AUC

AUC is more appropriate than accuracy for assessing the performance of imbalanced data classification. Let us consider an example with \(2\) positive data and \(100\) negative data. If one positive data has a prediction score \(0.5\) and another one has a prediction score \(-0.2\), and all negative data has prediction scores less than \(0\) but larger than \(-0.2\). In this case, if we choose a classification threshold as \(0\), then the accuracy is \(101/102=0.99\). However, the empirical AUC score according to (\(\ref{eqn:auc-emp}\)) is given by \(100/200=0.5\). “Can a model that optimizes the accuracy also optimize the AUC score?” Unfortunately, this is not the case as different classifiers that have the same accuracy could have dramatic different AUC. An example is illustrated in Table 2.2. Hence, it makes sense to directly optimize AUC.

Pairwise Surrogate Losses

Using a pairwise surrogate loss \(\ell(\cdot)\) of the indicator function \(\mathbb{I}(t\ge0)\) (see examples in Table 2.3, we have the following empirical AUC optimization problem for learning a parameterized function \(h(\mathbf{w};\cdot)\): \[\begin{align}\label{eqn:eaucd} \min_{\mathbf{w}\in\mathbb{R}^d}\frac{1}{n_+}\frac{1}{n_-}\sum_{\mathbf{x}_i\in\mathcal{S}_+}\sum_{\mathbf{x}_j\in\mathcal{S}_-}\ell(h(\mathbf{w};\mathbf{x}_j)-h(\mathbf{w};\mathbf{x}_i)). \end{align}\] This can be regarded as a special case of (\(\ref{eqn:xrisk}\)) by setting \[\begin{align*} &g(\mathbf{w};\mathbf{x}_i,\mathcal{S}_-)=\frac{1}{n_-}\sum_{\mathbf{x}_j\in\mathcal{S}_-}\ell(h(\mathbf{w};\mathbf{x}_j)-h(\mathbf{w};\mathbf{x}_i)),\\ &f_i(g)=g. \end{align*}\] This is the simplest form of EXM as \(f\) is just a linear function. An unbiased stochastic gradient can be easily computed based on a pair of data points consisting of a random positive and a random negative data point.

Compositional Objectives

An alternative approach to formulate AUC maximization is to decouple the pairwise comparison between positive and negative examples. A generic formulation is given by: \[\begin{equation}\label{eqn:aucminmax} \begin{aligned} \min_{\mathbf{w}\in\mathbb{R}^d,(a,b)\in\mathbb{R}^2}\quad &\frac{1}{|\mathcal{S}_+|}\sum_{\mathbf{x}_i\in\mathcal{S}_+}(h(\mathbf{w};\mathbf{x}_i)-a)^2+\frac{1}{|\mathcal{S}_-|}\sum_{\mathbf{x}_j\in\mathcal{S}_-}(h(\mathbf{w};\mathbf{x}_j)-b)^2\\ &+f\left(\frac{1}{|\mathcal{S}_-|}\sum_{\mathbf{x}_j\in\mathcal{S}_-}h(\mathbf{w};\mathbf{x}_j)-\frac{1}{|\mathcal{S}_+|}\sum_{\mathbf{x}_i\in\mathcal{S}_+}h(\mathbf{w};\mathbf{x}_i)\right), \end{aligned} \end{equation}\] where \(f\) is a non-linear function. The last component is a compositional function.

The above formulation also has a clear physical meaning. In particular, minimizing the first two terms aim to push the prediction scores of positive and negative examples to center around their means, respectively, and minimizing the third term aims to push the mean score of positive examples to be larger than the mean score of negative examples.

The above formulation is motivated by the pairwise formulation with a square surrogate function \(\ell(h(\mathbf{w};\mathbf{x}_j)-h(\mathbf{w};\mathbf{x}_i))=(c+h(\mathbf{w};\mathbf{x}_j)-h(\mathbf{w};\mathbf{x}_i))^2\). Indeed, in this case, (\(\ref{eqn:eaucd}\)) is equivalent to (\(\ref{eqn:aucminmax}\)) with \(f(s)=(s+c)^2\). We leave this as an exercise for interested readers. Nevertheless, using \(f(s)=[s+c]_+^2\) in (\(\ref{eqn:aucminmax}\)) is more robust than \(f(s)=(s+c)^2\) with \(c>0\).

Solving the above problem requires compositional optimization techniques, which will be discussed in Section 6.4.

Average Precision Loss

Area under precision-recall curve (AUPRC) is another commonly used measure for highly imbalanced data. The precision and recall of a scoring function \(h\) at threshold \(t\) are defined as \[\begin{align*} &\text{Rec}(t):=\Pr(h(\mathbf{x})>t\mid y=1)=\text{TPR}(t),\\ &\text{Prec}(t):=\Pr(y=1\mid h(\mathbf{x})>t). \end{align*}\] For a given \(u\in[0,1]\), let \(\text{TPR}^{-1}(u)=\inf\{t\in\mathbb{R}:\text{TPR}(t)\le u\}\). The precision–recall (PR) curve is defined as \(\{(u,\text{PR}(u))\}\), where \(u\in[0,1]\) and \(\text{PR}(u)=\text{Prec}(\text{TPR}^{-1}(u))\). Hence, AUPRC for \(h\) can be computed by \[ \text{AUPRC}(h)=\int_0^1\text{PR}(u)\,du. \]

■

The above theorem yields the following empirical estimator of AUPRC on a set of training examples \(\mathcal{S}=\mathcal{S}_+\cup\mathcal{S}_-\), known as average precision (AP): \[\begin{align}\label{eqn:AP} \text{AP}(h)=\frac{1}{n_+}\sum_{\mathbf{x}_i\in\mathcal{S}_+} \frac{\sum_{\mathbf{x}_j\in\mathcal{S}_+}\mathbb{I}(h(\mathbf{x}_j)\ge h(\mathbf{x}_i))} {\sum_{\mathbf{x}_j\in\mathcal{S}}\mathbb{I}(h(\mathbf{x}_j)\ge h(\mathbf{x}_i))}. \end{align}\] AP is an unbiased estimator of AUPRC in the limit \(n\to\infty\).

Necessity of Maximizing AUPRC

While AUC is generally more suitable than accuracy for imbalanced classification tasks, it may fail to adequately capture misorderings among top-ranked examples. Consider a scenario with \(2\) positive and \(100\) negative samples. If the two positive samples are ranked below just two of the negative ones, followed by the remaining \(98\) negatives, the resulting AUC is \(196/200=0.98\), which appears high. However, this model would be inadequate if our focus is on the top two predicted positive instances. In drug discovery, for example, models are expected to identify the most promising candidate molecules for experimental validation. If these top-ranked predictions turn out to lack the desired properties, the resulting experimental efforts may lead to significant wasted resources and costly failures.

To avoid this issue, AUPRC or its empirical estimator AP is typically used as a performance metric. According to (\(\ref{eqn:AP}\)), the AP score for the above example is \(\frac{1}{2}(\frac{1}{3}+\frac{2}{4})=0.42\). In contrast, a perfect ranking that ranks the two positive examples at the top gives an AP score of \(1\). Unfortunately, optimizing AUC does not necessarily lead to optimal AP, as two models with identical AUC scores can exhibit significantly different AP values. This highlights the need for efficient optimization algorithms that directly maximize AP.

Surrogate Loss of AP

To construct a differentiable objective for minimization, a differentiable surrogate loss \(\ell(h(\mathbf{x}_j)-h(\mathbf{x}_i))\) is used in place of \(\mathbb{I}(h(\mathbf{x}_j)\ge h(\mathbf{x}_i))\). Then AP can be approximated by: \[\begin{align}\label{eqn:AP-app} \text{AP}\approx\frac{1}{n_+}\sum_{\mathbf{x}_i\in\mathcal{S}_+} \frac{\sum_{\mathbf{x}_j\in\mathcal{S}}\mathbb{I}(y_j=1)\ell(h(\mathbf{x}_j)-h(\mathbf{x}_i))} {\sum_{\mathbf{x}_j\in\mathcal{S}}\ell(h(\mathbf{x}_j)-h(\mathbf{x}_i))}. \end{align}\]

Let us define \[\begin{align*} &f(\mathbf{g})=-\frac{[\mathbf{g}]_1}{[\mathbf{g}]_2},\\ &\mathbf{g}(\mathbf{w};\mathbf{x}_i,\mathcal{S})=[g_1(\mathbf{w};\mathbf{x}_i,\mathcal{S}),g_2(\mathbf{w};\mathbf{x}_i,\mathcal{S})],\\ &g_1(\mathbf{w};\mathbf{x}_i,\mathcal{S})=\frac{1}{|\mathcal{S}|}\sum_{\mathbf{x}_j\in\mathcal{S}}\mathbb{I}(y_j=1)\ell(h(\mathbf{w};\mathbf{x}_j)-h(\mathbf{w};\mathbf{x}_i)),\\ &g_2(\mathbf{w};\mathbf{x}_i,\mathcal{S})=\frac{1}{|\mathcal{S}|}\sum_{\mathbf{x}_j\in\mathcal{S}}\ell(h(\mathbf{w};\mathbf{x}_j)-h(\mathbf{w};\mathbf{x}_i)). \end{align*}\] Then, we formulate AP maximization as the following problem: \[\begin{align}\label{eqn:apsurr} \min_{\mathbf{w}}\frac{1}{n_+}\sum_{\mathbf{x}_i\in\mathcal{S}_+}f(\mathbf{g}(\mathbf{w};\mathbf{x}_i,\mathcal{S})), \end{align}\] which is a special case of EXM. We will explore efficient algorithms for optimizing AP in Section 6.4 using FCCO techniques.

Partial AUC Losses

There are two commonly used versions of partial AUC (pAUC), namely one-way pAUC (OPAUC) and two-way pAUC (TPAUC). OPAUC puts a restriction on the range of FPR, i.e., \(\text{FPR}\in[\alpha,\beta]\) (the second figure from the left in Figure 2.3) and TPAUC puts a restriction on the lower bound of TPR and the upper bound of FPR, i.e., \(\text{TPR}\ge\alpha\), \(\text{FPR}\le\beta\) (the second figure from the right in Figure 2.3).

By the definition, we have the following probabilistic interpretations.

Proof.
The first part about OPAUC is similar to AUC except for the range of integral: \[\begin{align*} \text{OPAUC}(h|\text{FPR}\in(\alpha,\beta)) &=\int_{\text{FPR}^{-1}(\beta)}^{\text{FPR}^{-1}(\alpha)}\text{TPR}(t)\,dF_-(t)\\ &=\int_{\text{FPR}^{-1}(\beta)}^{\text{FPR}^{-1}(\alpha)}\int_{-\infty}^{\infty}p_+(s)p_-(t)\mathbb{I}(s>t)\,ds\,dt. \end{align*}\] This concludes the proof of the first part.

■

Hence, an empirical estimator of OPAUC with FPR restricted in the range \([\alpha,\beta]\) can be computed by \[\begin{align}\label{eqn:opauc-emp} \frac{1}{n_+(k_2-k_1)}\sum_{\mathbf{x}_i\in\mathcal{S}_+}\sum_{\mathbf{x}_j\in\mathcal{S}_-^{\downarrow}[k_1+1,k_2]}\mathbb{I}(h(\mathbf{x}_i)>h(\mathbf{x}_j)), \end{align}\] where \(k_1=\lceil n_-\alpha\rceil,k_2=\lfloor n_-\beta\rfloor\), and \(\mathcal{S}^{\downarrow}[k_1,k_2]\subseteq\mathcal{S}\) denotes the subset of examples whose rank in terms of their prediction scores in the descending order are in the range \([k_1,k_2]\).

An empirical estimator of TPAUC with FPR restricted in a range of \([0,\beta]\) and TPR restricted in a range of \([\alpha,1]\) is computed by: \[\begin{align}\label{eqn:etpaucd2} \frac{1}{k_1}\frac{1}{k_2}\sum_{\mathbf{x}_i\in\mathcal{S}_+^{\uparrow}[1,k_1]}\sum_{\mathbf{x}_j\in\mathcal{S}_-^{\downarrow}[1,k_2]}\mathbb{I}(h(\mathbf{x}_i)>h(\mathbf{x}_j)), \end{align}\] where \(k_1=\lceil n_+(1-\alpha)\rceil,k_2=\lfloor n_-\beta\rfloor\), and \(\mathcal{S}^{\uparrow}[k_1,k_2]\subseteq\mathcal{S}\) denotes the subset of examples whose rank in terms of their prediction scores in the ascending order are in the range \([k_1,k_2]\).

Necessity of Maximizing partial AUC

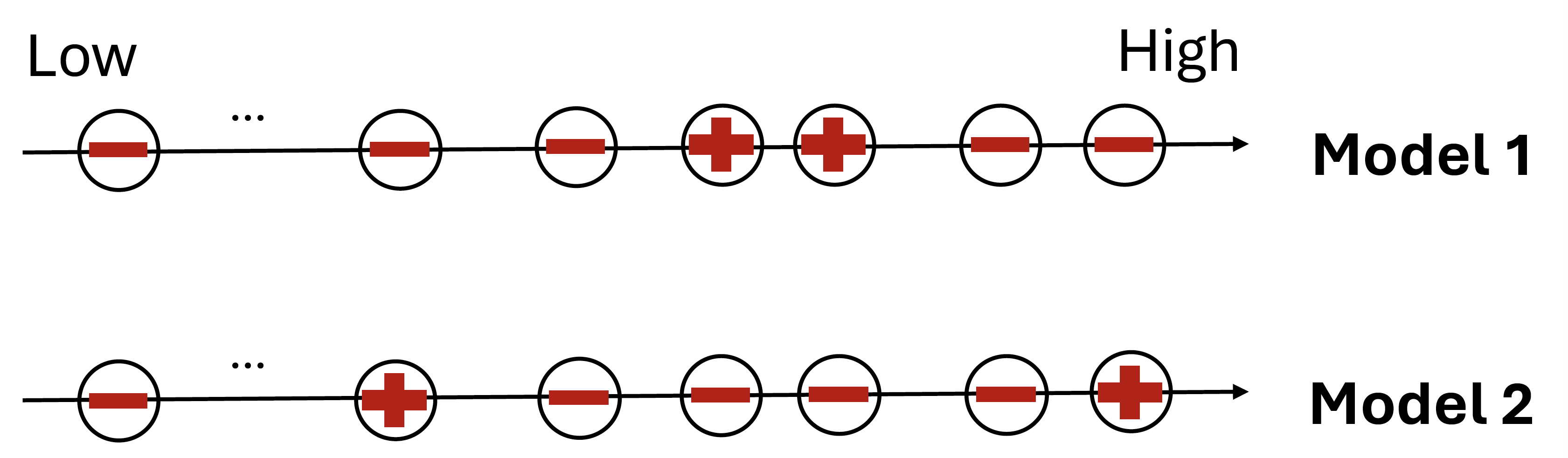
In many applications, there are large monetary costs due to high false positive rates (FPR) and low true positive rates (TPR), e.g., in medical diagnosis. Hence, a measure of interest would be the pAUC- the region of the ROC curve corresponding to low FPR and/or high TPR. With a similar argument as last section, a model that maximizes AUC does not necessarily optimizes pAUC. Let us compare two models on a dataset with \(2\) positive and \(100\) negative molecules (Figure 2.4). The model 1 ranks two negatives above the two positives followed by the remaining \(98\) negatives. The model 2 ranks one positive at the top, and then four negatives above the other positive followed by the remaining \(96\) negatives. The two models have the same AUC score of \(196/200=0.98\) but have different pAUC scores. When restricting \(\text{FPR}\in[0,0.02]\), model 1 has an empirical pAUC score of \(0/4=0\) and model 2 has an empirical pAUC score of \(2/4=0.5\) according to (\(\ref{eqn:opauc-emp}\)).

A Direct Formulation

Using a surrogate loss of zero-one loss, the maximization of OPAUC with FPR less than \(\beta\) for learning a parameterized model \(h(\mathbf w; \cdot)\) can be formulated as: \[\begin{align}\label{eqn-epaucd2} \min_{\mathbf{w}}\frac{1}{n_+}\frac{1}{k_2}\sum_{\mathbf{x}_i\in\mathcal{S}_+}\sum_{\mathbf{x}_j\in\mathcal{S}_-^{\downarrow}[1,k_2]}\ell(h(\mathbf{w};\mathbf{x}_j)-h(\mathbf{w};\mathbf{x}_i)). \end{align}\] Similarly, TPAUC maximization can be formulated as: \[\begin{align}\label{eqn-etpaucd2} \min_{\mathbf{w}}\frac{1}{k_1}\frac{1}{k_2}\sum_{\mathbf{x}_i\in\mathcal{S}_+^{\uparrow}[1,k_1]}\sum_{\mathbf{x}_j\in\mathcal{S}_-^{\downarrow}[1,k_2]}\ell(h(\mathbf{w};\mathbf{x}_j)-h(\mathbf{w};\mathbf{x}_i)), \end{align}\] where \(k_1=\lceil n_+(1-\alpha)\rceil,k_2=\lfloor n_-\beta\rfloor\).

Both problems are not standard ERM. The challenge for solving the above problems is that the selection of examples in a range, e.g., \(\mathcal{S}_-^{\downarrow}[1,k_2]\) and \(\mathcal{S}_+^{\uparrow}[1,k_1]\), is not only expensive but also non-differentiable. We will explore different approaches for optimizing OPAUC and TPAUC in Section 6.4 using advanced compositional optimization techniques.

An Indirect Formulation

When the surrogate loss \(\ell(t)\) is non-decreasing, the top-\(k\) selector of negative examples \(\mathcal{S}_-^{\downarrow}[1,k_2]\) can be transferred into the top-\(k\) average of pairwise losses, which becomes an CVaR. By drawing the connection between CVaR and KL-regularized DRO, an indirect objective for OPAUC maximization is formulated by: \[\begin{align}\label{eqn:epaucd3} \min_{\mathbf{w}}\frac{1}{n_+}\sum_{\mathbf{x}_i\in\mathcal{S}_+}\tau\log\left(\frac{1}{n_-}\sum_{\mathbf{x}_j\in\mathcal{S}_-}\exp\left(\frac{\ell(h(\mathbf{w};\mathbf{x}_j)-h(\mathbf{w};\mathbf{x}_i))}{\tau}\right)\right). \end{align}\] This problem is an instance of EXM, which will be solved by FCCO techniques. TPAUC maximization can be handled similarly. We will present detailed exposition in Section 6.4.

Ranking Losses

Ranking losses are commonly employed in learning to rank.

Let \(\mathcal{Q}\) denote the query set of size \(N\), and let \(q\in\mathcal{Q}\) represent an individual query. For each query \(q\), let \(\mathcal{S}_q\) be a set of \(N_q\) items (e.g., documents, movies) to be ranked. For each item \(\mathbf{x}_{q,i}\in\mathcal{S}_q\), let \(y_{q,i} \in \mathbb R^+\) denote its relevance score, typically an integer grade such as \(0,1,2,\ldots\), which quantifies the relevance between the query \(q\) and the item \(\mathbf x_{q,i}\). Define \(\mathcal{S}_q^+\subseteq\mathcal{S}_q\) as the subset of \(N_q^+\) items relevant to \(q\), i.e., those with non-zero relevance scores. Let \(\mathcal{S}=\{(q,\mathbf{x}_{q,i})\mid q\in\mathcal{Q},\mathbf{x}_{q,i}\in\mathcal{S}_q^+\}\) represent the collection of all relevant query-item (Q-I) pairs.

Let \(s(\mathbf{w};\mathbf{x},q)\) denote the predicted relevance score for item \(\mathbf{x}\) with respect to query \(q\), parameterized by \(\mathbf{w}\in\mathbb{R}^d\) (e.g., a deep neural network). Define the rank of item \(\mathbf{x}\) within \(\mathcal{S}_q\) as: \[\begin{align*} r(\mathbf{w};\mathbf{x},\mathcal{S}_q)=\sum_{\mathbf{x}'\in\mathcal{S}_q}\mathbb{I}(s(\mathbf{w};\mathbf{x}',q)-s(\mathbf{w};\mathbf{x},q)\ge0), \end{align*}\] where ties are ignored.

NDCG and NDCG Loss

Normalized Discounted Cumulative Gain (NDCG) is a metric commonly used to evaluate the quality of ranking algorithms, especially in information retrieval and recommender systems.

NDCG evaluates how well a model ranks relevant items near the top of a list for a query \(q\). The DCG of a ranked list according to \(\{s(\mathbf{w};\mathbf{x},q),\mathbf{x}\in\mathcal{S}_q\}\) is given by: \[ \text{DCG}_q:=\sum_{\mathbf{x}\in\mathcal{S}_q}\frac{2^{y_i}-1}{\log_2(1+r(\mathbf{w};\mathbf{x},\mathcal{S}_q))} =\sum_{\mathbf{x}\in\mathcal{S}_q^+}\frac{2^{y_i}-1}{\log_2(1+r(\mathbf{w};\mathbf{x},\mathcal{S}_q))}. \] Note that the summation is over \(\mathcal{S}_q^+\) rather than \(\mathcal{S}_q\), as only relevant items contribute to the DCG score due to their non-zero relevance.

NDCG normalizes DCG by the ideal DCG denoted by \(Z_q\) of the best possible ranking: \[ \text{NDCG}_q=\frac{\text{DCG}_q}{Z_q}. \] The average NDCG over all queries is given by: \[\begin{align}\label{eqn:NDCG} \text{NDCG:}\quad\frac{1}{N}\sum_{q=1}^N\frac{1}{Z_q}\sum_{\mathbf{x}_{q,i}\in\mathcal{S}_q^+}\frac{2^{y_{q,i}}-1}{\log_2(r(\mathbf{w};\mathbf{x}_{q,i},\mathcal{S}_q)+1)}, \end{align}\] where \(Z_q\) can be precomputed.

By replacing the indicator function with a surrogate function in Table 2.3, we approximate \(r(\mathbf{w};\mathbf{x},\mathcal{S}_q)/N_q\) by \[ g(\mathbf{w};\mathbf{x},\mathcal{S}_q)=\frac{1}{N_q}\sum_{\mathbf{x}'\in\mathcal{S}_q}\ell(s(\mathbf{w};\mathbf{x}',q)-s(\mathbf{w};\mathbf{x},q)). \] Then the NDCG loss minimization is defined by \[\begin{align}\label{eqn:NDCG-loss} \min_{\mathbf{w}}\frac{1}{N}\sum_{q=1}^N\frac{1}{Z_q}\sum_{\mathbf{x}_{q,i}\in\mathcal{S}_q^+}\frac{1-2^{y_{q,i}}}{\log_2(N_q g(\mathbf{w};\mathbf{x}_{q,i},\mathcal{S}_q)+1)}, \end{align}\] which is an instance of EXM. We will explore FCCO techniques for solving this problem in Section 6.4.

Listwise Cross-Entropy Loss

Analogous to multi-class classification, we can define a listwise cross-entropy loss for ranking. This is based on modeling the probability that a specific item is ranked at the top: \[\begin{align}\label{eqn:dpm-list} P_{\text{top}}(\mathbf{x}\mid q)=\frac{\exp(s(\mathbf{w};\mathbf{x},q))}{\sum_{\mathbf{x}_j\in\mathcal{S}_q}\exp(s(\mathbf{w};\mathbf{x}_j,q))}. \end{align}\] Accordingly, the listwise cross-entropy loss for query \(q\) is defined as: \[\begin{align*} L(\mathbf{w};q)=\sum_{\mathbf{x}_{q,i}\in\mathcal{S}_q^+}-p_{q,i}\log\left(\frac{\exp(s(\mathbf{w};\mathbf{x}_{q,i},q))}{\sum_{\mathbf{x}_j\in\mathcal{S}_q}\exp(s(\mathbf{w};\mathbf{x}_j,q))}\right), \end{align*}\] where \(p_{q,i}\) denotes the top-one prior probability for item \(\mathbf{x}_{q,i}\), such as \[ p_{q,i} = \frac{\exp(y_{q,i})}{\sum_{\mathbf x_{q,i} \in \mathcal S_q} \exp(y_{q,i})} \quad \text{or} \quad p_{q,i} = \frac{y_{q,i}}{\sum_{\mathbf x_{q, i}\in\mathcal S_q}y_{q,i}}. \]

An optimization objective based on the average of listwise cross-entropy losses over all queries leads to the following formulation known as ListNet: \[\begin{align}\label{eqn:listnet} \min_{\mathbf{w}}\quad\frac{1}{N}\sum_{q=1}^N\sum_{\mathbf{x}_{q,i}\in\mathcal{S}_q^+}p_{q,i}\log\left(\sum_{\mathbf{x}_j\in\mathcal{S}_q}\exp(s(\mathbf{w};\mathbf{x}_j,q)-s(\mathbf{w};\mathbf{x}_{q,i},q))\right). \end{align}\]

This formulation closely resembles equation (\(\ref{eqn:epaucd3}\)) and constitutes a special case of the EXM framework.

Contrastive Losses

Contrastive losses are commonly used in representation learning, which is a fundamental problem in the era of deep learning and modern AI.

A deep neural network is usually used to extract representation from unstructured raw data. Let \(h(\mathbf{w};\cdot):\mathcal{X}\to\mathbb{R}^{d_1}\) denote the representation network that outputs an embedding vector, which is sometimes called the encoder. A meaningful encoder should capture the semantics such that `similar’ data points (positive pairs) are closer to each other and dissimilar data points (negative pairs) are far away from each other in the embedding space.

To conduct the representation learning, the following data is usually constructed. Let \(\mathbf{x}_i\) be an anchor data, and let \(\mathbf{x}_i^+\) denote a positive data of \(\mathbf{x}_i\). Denote by \(\mathcal{S}_i^-\) the set of negative data of \(\mathbf{x}_i\). Let \(s(\mathbf{w};\mathbf{x},\mathbf{y})\) denote a similarity score between the two encoded representations. For example, if \(h(\mathbf{w};\mathbf{x})\) is a normalized vector such that \(\|h(\mathbf{w};\mathbf{x})\|_2=1\), we can use \(s(\mathbf{w};\mathbf{x},\mathbf{y})=h(\mathbf{w};\mathbf{x})^{\top}h(\mathbf{w};\mathbf{y})\).

A contrastive loss for each positive pair \((\mathbf{x}_i,\mathbf{x}_i^+)\) is defined by: \[\begin{align}\label{eqn:GCL1} L(\mathbf{w};\mathbf{x}_i,\mathbf{x}_i^+)=\tau\log\left(\frac{1}{|\mathcal{S}_i^-|}\sum_{\mathbf{y}\in\mathcal{S}_i^-}\exp((s(\mathbf{w};\mathbf{x}_i,\mathbf{y})-s(\mathbf{w};\mathbf{x}_i,\mathbf{x}_i^+))/\tau)\right), \end{align}\] where \(\tau>0\) is called the temperature parameter. Given a set of data \(\{(\mathbf{x}_i,\mathbf{x}_i^+,\mathcal{S}_i^-)\}_{i=1}^n\), minimizing a contrastive objective for representation learning is formulated as: \[\begin{equation}\label{eqn:GCL} \begin{aligned} \min_{\mathbf{w}}\quad \frac{1}{n}\sum_{i=1}^n\tau\log\left(\frac{1}{|\mathcal{S}_i^-|}\sum_{\mathbf{y}\in\mathcal{S}_i^-}\exp((s(\mathbf{w};\mathbf{x}_i,\mathbf{y})-s(\mathbf{w};\mathbf{x}_i,\mathbf{x}_i^+))/\tau)\right). \end{aligned} \end{equation}\]

Traditional supervised representation learning methods construct the positive and negative data using the annotated class labels, such that data in the same class are deemed as positive and data from different classes are considered as negative. However, this requires a large amount of labeled data to learn a deep encoder, which requires significant human effort in labeling. To address this issue, self-supervised representation learning (SSRL) techniques are employed to fully exploit the vast data readily available on the internet via self-supervision to learn representations that are useful for many downstream tasks. In SSRL, a positive pair \((\mathbf{x}_i,\mathbf{x}_i^+)\) may consist of different augmented views of the same sample or represent different modalities of the same underlying object (e.g., an image and its corresponding text caption). The negative samples for each anchor \(\mathbf{x}_i\) are typically drawn from all other data points in the dataset excluding \(\mathbf{x}_i\). In this setting, a variant of the contrastive objective is useful by adding a small constant \(\varepsilon>0\) inside the logarithm: \[\begin{equation}\label{eqn:GCLN} \begin{aligned} \min_{\mathbf{w}}\quad \frac{1}{n}\sum_{i=1}^n\tau\log\left(\varepsilon+\frac{1}{|\mathcal{S}_i^-|}\sum_{\mathbf{y}\in\mathcal{S}_i^-}\exp((s(\mathbf{w};\mathbf{x}_i,\mathbf{y})-s(\mathbf{w};\mathbf{x}_i,\mathbf{x}_i^+))/\tau)\right). \end{aligned} \end{equation}\] This can mitigate the impact of false negative data in \(\mathcal{S}_i^-\). We will explore SSRL in Section 6.4..

Optimization Challenge

Optimizing the above contrastive objectives is challenging due to the presence of summations both inside and outside the logarithmic function. These losses can be reformulated as special cases of the X-risk, where the outer function is \(f(g_i)=\tau\log(g_i)\), and \(g_i\) represents the inner average computed over negative samples associated with each \(\mathbf{x}_i\).

← Go Back