Preface
“知者行之始,行者知之成” — 王阳明
“The best theory is inspired by practice.
The best practice is inspired by theory.”
— Donald Knuth
Optimization is central to machine learning (ML), which in turn forms the foundation of artificial intelligence (AI). From training deep neural networks to fine-tuning Large Language Models, almost every advancement in AI relies on solving some form of optimization problem. While classical methods based on empirical risk minimization (ERM) have powered much of early progress in ML, they are no longer sufficient to address the growing complexity of today’s AI challenges. This book aims to bridge that gap by offering a systematic treatment of the emerging optimization paradigm known as compositional optimization and its applications in modern AI.
Many critical optimization problems in ML now exhibit intricate compositional structures such as $f(g)$ or $\sum_{i}f_i(g_i)$ that go beyond traditional frameworks, where both $f$ and $g$ are non-linear and potentially non-convex—extending beyond the scope of classical optimization. However, most existing texts remain focused on classical stochastic optimization and ERM, overlooking the depth and diversity of these newer challenges.
Motivation for Writing the Book
Optimization once held a central spotlight at leading ML venues such as NeurIPS and ICML. In recent years, however, the field has seen an influx of new topics in AI, capturing the interest of students and early-career researchers. While attention has increasingly shifted toward foundation models and AGI, the importance and impact of optimization remain as vital as ever.
As someone working at the intersection of optimization and machine learning, I feel a dual responsibility.
First, to bring cutting-edge optimization techniques to the broader ML/AI community. When I speak with researchers in ML/AI and mention my focus on optimization for machine learning, I am often met with questions like, “What problems are you working on?” or “Are these theories truly useful, given that they rely on assumptions that may not hold in practice?” Some even remark that optimization’s only practical contribution to AI is the Adam algorithm. This reflects a common misconception that optimization in ML is limited to training algorithms like SGD or Adam, which is far from the truth.
Second, I feel a responsibility to encourage researchers in mathematical optimization to engage more deeply with the challenges of modern AI. Many researchers in traditional optimization are eager to contribute, but the rapid pace of AI along with the constant influx of new models and terminology can make it difficult to identify core problems where optimization insights are most needed. Working at this intersection gives me a unique perspective: I can recognize fundamental challenges in modern AI, such as the training of large foundation models, and abstract them into rigorous mathematical frameworks where optimization methods can offer meaningful solutions.
I hope this book contributes to bridging the gap between the AI and optimization communities and inspires new collaborations across these fields.
At first glance, the focus on compositional optimization in this book may seem narrow, but it is deeply connected to fundamental learning and optimization principles including discriminative learning and robust optimization, and has broad applicability across ML and modern AI, which will be shown in this book. In particular, this book introduces a new family of risk functions termed X-risks, in which the loss function of each data involves comparison with many others. We formulate empirical X-risk minimization as finite-sum coupled compositional optimization (FCCO) - a new family of compositional optimization. After five years of intensive research on this subject, we have explored different aspects of FCCO, from upper bounds to lower bounds, from smooth objectives to non-smooth objectives, from convex problems to non-convex problems, and from theoretical complexity analysis to applications in training large foundation models. While significant progress has been made, many open questions remain. Nevertheless, we believe it is time to share this advanced body of knowledge with the broader community in the form of a comprehensive book.
Structure of the Book
This book is crafted to engage both theory-oriented and practice-driven audiences. It presents rigorous theoretical analysis with deep insights, complemented by practical implementation tips, GitHub code repositories, and empirical evidence—effectively bridging the gap between theory and application.
It is intended for graduate students, applied researchers, and anyone interested in the intersection of optimization and machine learning. Readers are assumed to have some basic knowledge in ML. The materials in this book have been used in my graduate-level course on stochastic optimization for ML.
The book is organized as follows:
- Chapter 1: Reviews the fundamentals of convex optimization essential for the rest of the book.
- Chapter 2: Introduces advanced learning methods that go beyond the traditional ERM framework to motivate compositional optimization.
- Chapter 3: Presents classical stochastic optimization algorithms and their complexity analysis in both convex and non-convex settings.
- Chapter 4: Delves into stochastic compositional optimization (SCO) problems with algorithms and theoretical analysis.
- Chapter 5: Explores algorithms and complexity analysis for solving FCCO problems.
- Chapter 6: Presents applications of SCO and FCCO in supervised and self-supervised learning for training predictive models, generative models, and representation models.
- Chapter 7: Presents some afterwords.
The dependencies and flow among the chapters are illustrated in Figure. Practitioners may focus on Chapter 2 and Chapter 6. For theory-oriented audiences who are interested in ML applications, I strongly recommend reading Chapter 2 and Chapter 6 as well. Practitioners may focus on Chapters 2 and 6. For theory-oriented audiences interested in ML applications, Chapters 2 and 6 are also highly recommended.
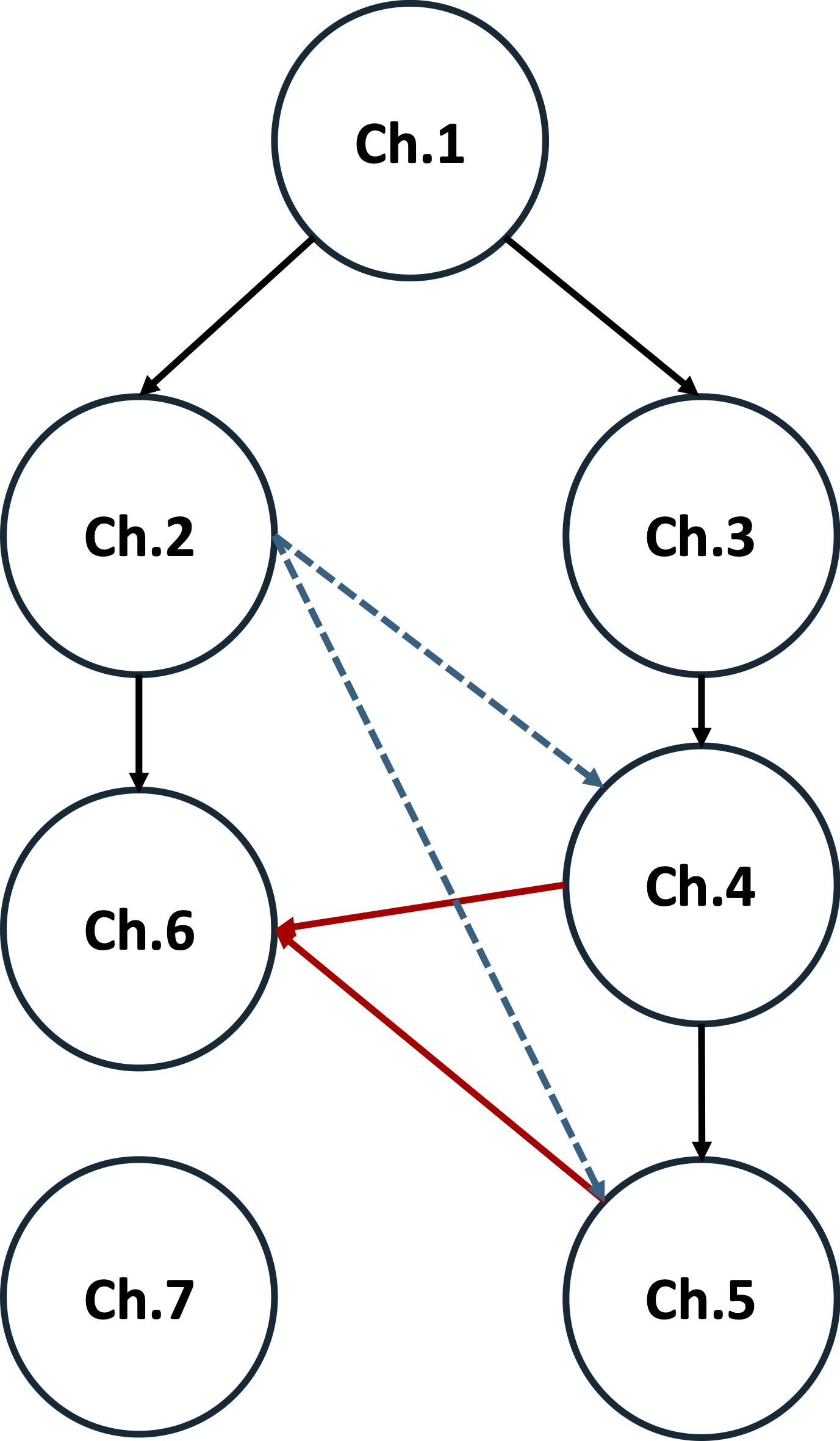
Figure: Structure of the book chapters. Dashed lines indicate motivation. Red solid lines indicate application. Other solid lines indicate dependency.
Acknowledgments
This book would not have been possible without the dedication and contributions of my students. I would like to thank my former and current Ph.D. students, visiting students, and postdocs who contributed to both the theoretical and empirical results presented in the book.
Theoretical contributions from:
Bokun Wang, Quanqi Hu, Zhishuai Guo, Yan Yan, Qi Qi, Wei Jiang, Ming Yang, Xingyu Chen, Yao Yao, Yi Xu, Mingrui Liu, and Linli Zhou.
Empirical contributions from:
Zhuoning Yuan, Gang Li, Xiyuan Wei, Dixian Zhu, Siqi Guo, Zihao Qiu, and Vicente Balmaseda.
Special thanks go to Bokun Wang for his help in preparing lecture notes and Quanqi Hu for polishing several proofs included in the book. I thank Ning Ning for proofreading some chapters.
I would like to thank my long-term collaborator Qihang Lin, with whom I worked on FCCO for constrained optimization featured in this book.
I am grateful to my academic collaborators Qihang Lin, Yiming Ying, Lijun Zhang, Tuo Zhao, Yunwen Lei, Shuiwang Ji, Nitesh Chawla, Zhaosong Lu, Jiebo Luo, Xiaodong Wu, My T. Thai, Milan Sonka, Zhengzhong Tu, Tomer Galanti, Yinbing Liang, Hongchang Gao, Bang An, Ilgee Hong, Guanghui Wang, Limei Wang, Youzhi Luo, Haiyang Yu, and Zhao Xu, and industrial collaborators Rong Jin, Wotao Yin, Denny Zhou, Wei Liu, Xiaoyu Wang, Ming Lin, Liangliang Cao, Xuanhui Wang, Yuexin Wu, and Xianzhi Du.
Special thanks to Guanghui Lan, Chih-Jen Lin, and Stephen Wright for their insightful discussions on subjects covered in this work. I am especially thankful to My T. Thai for encouraging me to publish this book.
I owe a great debt of gratitude to my PhD advisor, Dr. Rong Jin, who introduced me to the world of optimization and taught me the value of focus.
I am deeply grateful to my department head at Texas A&M, Scott Schaefer, as well as to all my colleagues in the Department of Computer Science and Engineering, for fostering such a positive and collaborative atmosphere. I also like to thank my former colleagues at the University of Iowa.
Finally, I am grateful for support from the National Science Foundation under my CAREER award #1844403, the RI core grant #2246756, and the FAI grant #2246757.
College Station, TX, USA
Tianbao Yang
Janaury, 2026